

Next: Prelab Part I: AM
Up: Labs 6 and 7
Previous: Labs 6 and 7
Modulation is the modification of some aspect of a carrier signal. Given a signal of the form
where 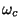 is known as the carrier frequency. If
is known as the carrier frequency. If 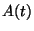 varies linearly with the modulating signal (your message to be transmitted), then we have linear modulation. If
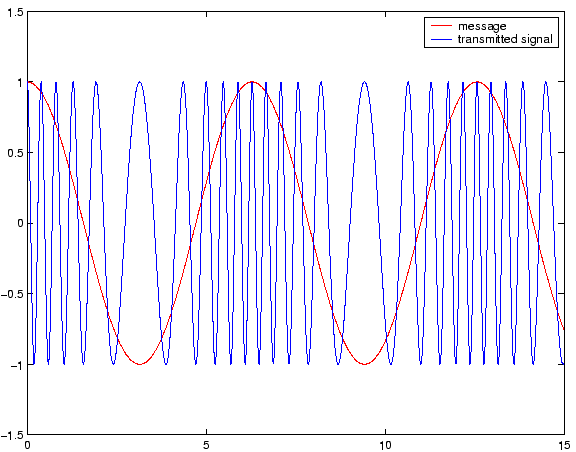
varies linearly with the modulating signal (your message to be transmitted), then we have linear modulation. If 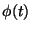 varies with the modulating signal, then we have angle modulation. Figures 1, 2 and 3, show modulated signals using amplitude modulation, phase modulation and frequency modulation, respectively. As seen in Figure 1, the message signal is modifying the amplitude of the carrier signal, hence the name amplitude modulation. In Figure 2, the oscillation increased or decreased based on the slope of the modulating signal. In Figure 3, the amplitude of the signal is modifying the rate of oscillation of the carrier signal.
varies with the modulating signal, then we have angle modulation. Figures 1, 2 and 3, show modulated signals using amplitude modulation, phase modulation and frequency modulation, respectively. As seen in Figure 1, the message signal is modifying the amplitude of the carrier signal, hence the name amplitude modulation. In Figure 2, the oscillation increased or decreased based on the slope of the modulating signal. In Figure 3, the amplitude of the signal is modifying the rate of oscillation of the carrier signal.
Figure 1:
Amplitude modulation
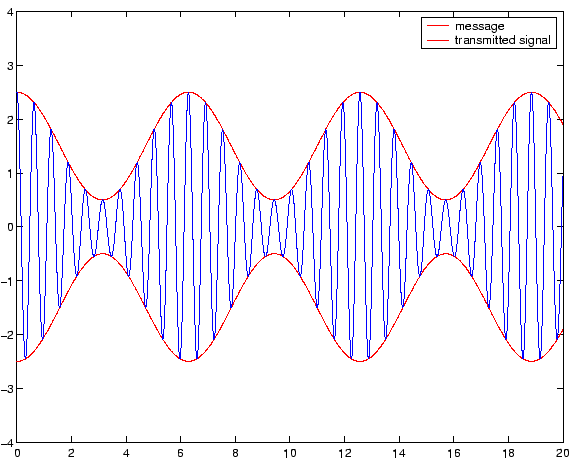 |
Figure 2:
Phase modulation
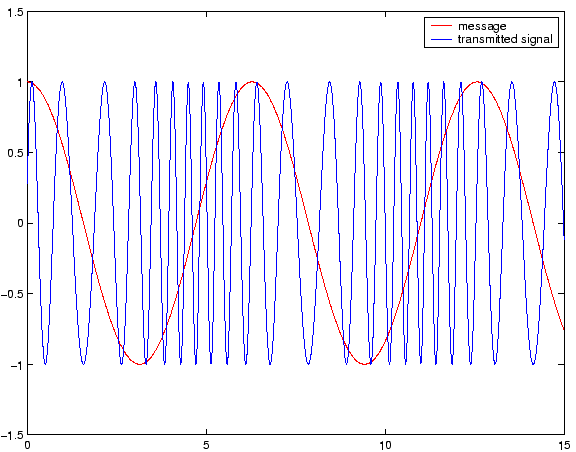 |
Figure 3:
Frequency modulation
 |
In this lab you will design an AM modulator/demodulator. An AM signal is of the form
It is important to choose 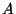 so that
so that
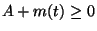 you will see why in the lab.
you will see why in the lab.


Next: Prelab Part I: AM
Up: Labs 6 and 7
Previous: Labs 6 and 7
Copyright © 2004, Aly El-Osery
Last Modified 2004-10-23