Prelab Part II: AM Demodulation

There are several ways to demodulate an AM signal. The one that will be used here is using a square law detector. The way this works is by taking the AM signal, square the signal and then pass it through a lowpass filter.

1. Given

   $$x_c(t)=[A+m(t)]\cos(\omega_ct)$$

   
   
   show that you will be able to recover 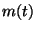$m(t)$ if you square 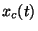$x_c(t)$ and then pass it through a lowpass filter.
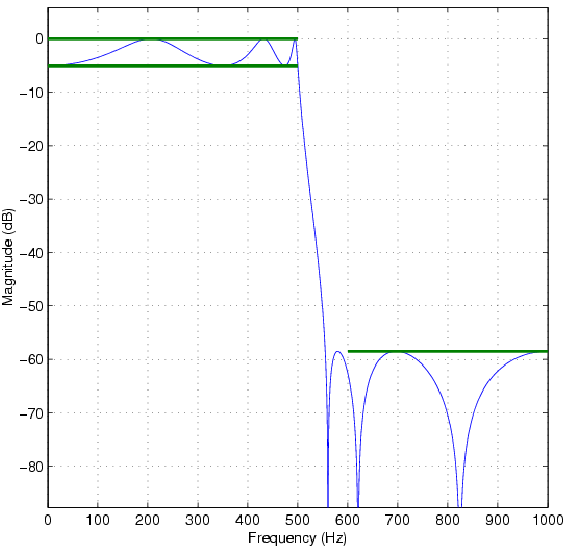
2. Figure 4 shows the magnitude characteristics of a physically realizable filter. On the the figure identify: (a) where is the passband, (b) where is the stopband, and (c) where is the transition band. Also, using the figure explain what is meant by passband ripple and stopband ripple.

   Figure 4: Elliptic filter design specifications

   

3. Use MATLAB to create an elliptic filter with the following specifications: 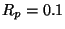$R_p=0.1$dB and 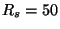$R_s=50$dB. What is the order of the filter?
4. Use MATLAB to express the filter as a cascade of second-order systems. You can use the tf2sos function.