EE 101
Pre-Lab Exercise 3
ALL GRAPHS MUST BE FULLY LABELED AND DRAWN NEATLY!
NO ANSWERS ARE COMPLETE WITHOUT THE UNITS! AS ALWAYS, SHOW YOUR WORK!
ALL GRAPHS MUST BE FULLY LABELED AND DRAWN NEATLY!
NO ANSWERS ARE COMPLETE WITHOUT THE UNITS! AS ALWAYS, SHOW YOUR WORK!

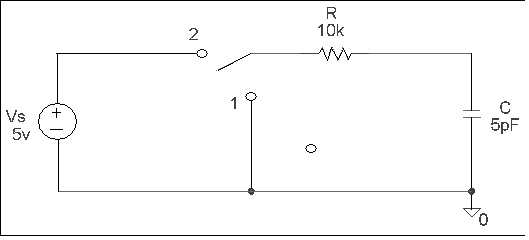
For part 3, assume the switch has been closed for a long time. At t = 0s, the switch is opened and the capacitor begins to discharge.
(end of pre-lab)
The purpose of this lab is to analyze an RC network using PSPICE.
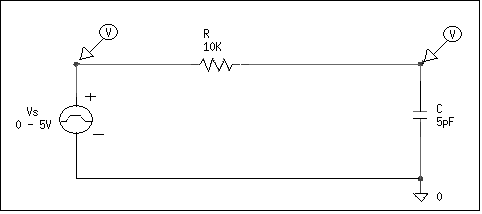
Figure 1
Unlike last week, the voltage source you will use will be a 0 to 5v pulse signal (Vpulse). The purpose of the pulse is to model a switch opening and closing. When the pulse is low (0 volts), the switch is modeled as open and when the pulse is high (5 volts), the switch is modeled as closed. You will need to define the parameters of the pulse. For the purpose of this exercise, you will inject a waveform that is 5 volts for the first 500 ns and 0 volts for the next 500 ns. To accomplish this, double click on the Vpulse symbol and enter the following attributes: V1 = 0V, V2 = 5V, TD = 0, TR = 0, TF = 0, PW = 0.5us, and PER = 1us. (TR = risetime, TF = falltime, TD = delay time, PW = pulse width, and PER = period of waveform)
Notice there are two voltage level markers on the schematic. These are used in the probe feature of PSPICE. Probe allows the user to observe how a circuit affects a signal. Specifically, you will observe how a 5 volt source charges the capacitor in an RC network (and how the capacitor discharges in the same network). Place the voltage markers on your schematic--one to measure the source voltage and one to measure the capacitor voltage (under the Markers menu, choose Mark Voltage/Level).
Before you simulate this circuit, make sure your analysis setup is correct. Under the Analysis menu, go to Setup and check to see that the Bias Point Detail and Transient options are enabled.
Perform an Electrical Rule Check and simulate your circuit. After a bit, the MicroSim Probe window will appear. It should look like this (Figure 2).
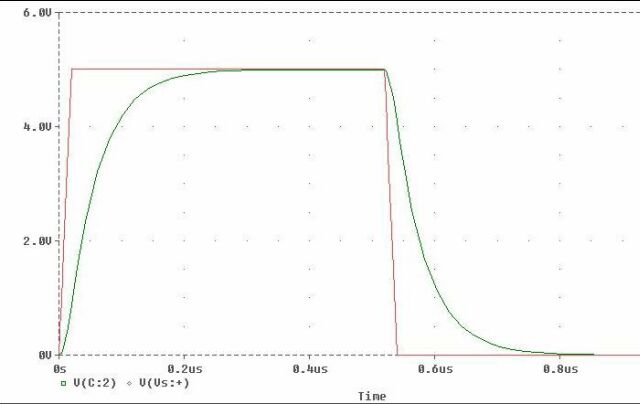
Figure 2
Notice that while the pulse reads 5 volts from 0 s to 500 ns, the capacitor is shown to be charging, while during the low portion of the pulse wave (500 ns to 1 us) the capacitor is discharging.
Add a set of cursors to the probe output (Tools - Cursor - Display). Click the right mouse button to display one set of vertical crosshairs. To make these crosshairs stick to the capacitor voltage curve, go down to the curve label (V(C:2)) and use the same mouse button to click on the small diamond to the left of the label. In the same way, but using the left mouse button, add the second cursor. This time, click on the diamond with the left mouse button to make the cursor stick to the charging curve.
Eqn. 1
where VC represents the capacitor voltage, VT the maximum capacitor voltage, and RC the time constant for the circuit. Another rule of thumb states that it takes the time of 5 time constants for a capacitor to "fully" charge or discharge. This value would be 250 ns for this circuit. Substituting the known quantities of t = 250 ns, RC = 50 ns, and VT = 5 volts into equation (1) results in VC = 4.97 volts, or 99% of the maximum possible voltage.
Move one cursor to the origin and the other cursor to the 99% position (4.97 volts) of the charge curve. Be as accurate as you can. Read the elapsed time it takes for the curve to rise from 0 volts to this position. Divide this value by 5 to determine the time constant value for the circuit. Does this number basically agree with the RC time constant value you calculated in the pre-lab?
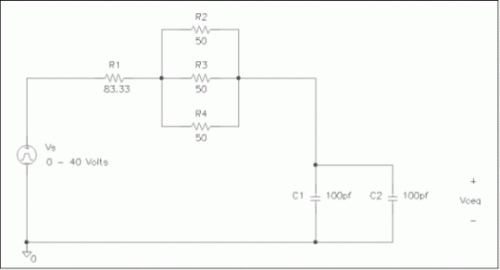
Figure 3
When your probe results are displayed, notice that the input pulse is repeated until it gets to the 1.0 us mark. Your first simulation you ran today used up the same amount of time, as well. However, that pulse was of a lower frequency and thus took up the entire span. Over three of the present pulses can fit in the 1.0 us time span because it is of shorter duration. The evaluation copy of PSPICE that you are using appears to be limited to 1.0 us worth of data analysis.
Like before, determine the time constant for this circuit by using the two "rule of thumb methods. Print out a copy of your plot that shows the cursors in the 10% and 90% of total voltage amplitude positions. On this plot, add a label with the time constant information and your name. Tape the printout into your lab book.
Copy over the following file to your U:\ drive (to U:\ee101\lab3 for instance):
N:\ee101\lab3\rccurve.m
This is a MATLAB "m-file" that contains a sequence of commands. If MATLAB is instructed to run on a m-file, it executes the commands contained in this file for you.
Using a text editor like NOTEPAD, edit this file. Look through the entire file and make sure you understand what is going on (should not be too hard considering it is well commented). You will need to edit this file to plot the charge/discharge for your circuits in Figures 1 and 3. Print and put these into your lab book.