Choosing the Clock for the HC12 PWM

HC12 - Two Choices of Clock for PWM

1.

PCLKx = 0:

${\rm Clk}_{\rm {x}} = 0.125 \mu{\rm {s}} \times 2^N$
${\rm Per}_{\rm {x}} = 0.125 \mu{\rm {s}} \times 2^N \times ({\tt {PWPERx+1}})$

2.

PCLKx = 1:

${\rm Clk}_{\rm {x}} = 0.125 \mu{\rm {s}} \times 2^{(N+1)} \times (M+1)$
${\rm Per}_{\rm {x}} = 0.125 \mu{\rm {s}} \times 2^{(N+1)} \times (M+1) \times ({\tt {PWPERx+1}})$

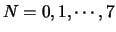
N = PCKA 2:0 for PWM 1 and 0, $N = 0, 1, \cdots, 7$
N = PCKB 2:0 for PWM 3 and 2.

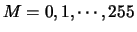
M = PWSCAL0 7:0 for PWM 1 and 0, $M = 0, 1, \cdots, 255$
M = PWSCAL1 7:0 for PWM 3 and 2.

Normally want PWPERx = 200 -> 255.

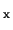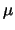Example: Want 5 kHz PWM - Per $_{\rm {x}}$ = 200 $\mu$ s.

1.

Try PCLKx = 0 and PWPERx = 255

$\begin{displaymath}200 \mu{\rm {s}} = 0.125 \mu{\rm {s}} \times 2^N \times ({\tt {PWPERx+1}})\end{displaymath}$

$\begin{displaymath}2^N = \frac{200 \mu{\rm {s}}}{0.125 \mu{\rm {s}} \times 256} = 6.25\end{displaymath}$

Not possible Try PWPERx = 199

$\begin{displaymath}2^N = \frac{200 \mu{\rm {s}}}{0.125 \mu{\rm {s}} \times 200} = 8\end{displaymath}$

N = 3

Exactly 5 kHz, get 1 part in 200 accuracy

2.

Try PCLKx = 1 and PWPERx = 255

$\begin{displaymath}200 \mu{\rm {s}} = 0.125 \mu{\rm {s}} \times 2^{(N+1)} \times (M+1) \times ({\tt {PWPERx+1}})\end{displaymath}$

$\begin{displaymath}2^{(N+1)} \times (M+1) = \frac{200 \mu{\rm {s}}}{0.125 \mu{\rm {s}} \times 256} = 6.25\end{displaymath}$

Not possible. Use a slightly different frequency - let

$\begin{displaymath}2^{(N+1)} \times (M+1) = 6\end{displaymath}$

$\begin{displaymath}N = 0 {\rm\ and \ } M = 2\end{displaymath}$

This gives

$\begin{displaymath}{\rm Per}_{\rm {x}} = 0.125 \mu{\rm {s}} \times 2^{(0+1)} \times (2+1) \times (255+1) = 192 \mu{\rm {s}}\end{displaymath}$

for a 5.2 kHz frequency

1999-03-09