%
% Filename: example6m
%
% Description: M-file to demonstrate digital PID control of a geared
% DC motor.
%
figure(1) % put plot in figure 1
clf; % clear figure & memory
clear;
tmax = 0.3; % amount of time to run simulation
T = 0.001; % sample interval
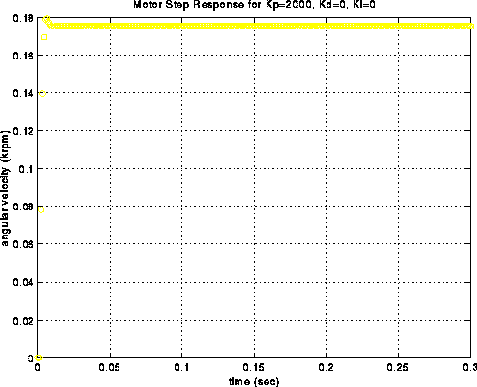
Kp = 2000; % proportional controller gain
Kd = 0.0; % derivative controller gain
Ki = 0.0; % integral controller gain
wd = 0.18; % desired angular velocity (krpm)
eint = 0; % initialize error integral to zero
eprev1 = 0; % initialize past values of error
eprev2 = 0; % to zero
KT = 4.07; % motor torque constant
L = 0.00156; % motor inductance
J = 2.0; % motor rotor & load inertia
R = 1.89; % motor resistance
B = 13.0; % motor/gear/bearing friction
Kb = 3.01; % motor back emf constant
N = 6/1; % gear ratio
wprev1 = 0; % w[1] = w(0) = 0
wprev2 = 0; % w[0] = wdot(0)*T + w(0)
woprev1 = wprev1/N; % initial values for output
woprev2 = wprev2/N; % shaft speed
for n=2:tmax/T,
eprev2 = (wd - woprev2); % define errors
eprev1 = (wd - woprev1);
eint = eint + (eprev1 + eprev2)*T/2; % integrate e using trapezoidal rule
eder = (eprev1 - eprev2)/T; % differentiate e using Euler approx.
vaprev2 = Kp*eprev2 + Kd*eder + Ki*eint; % compute input voltage
w = (2-(R*J+B*L)*T/(L*J))*wprev1 + ...
((R*J+B*L)*T/(L*J) - 1 - (B*R+KT*Kb)*T*T/(L*J))*wprev2 + ...
KT*T*T/(L*J)*vaprev2; % DC motor difference eqn
wprev2 = wprev1; % store values for next iteration
wprev1 = w;
wo = w/N; % convert motor speed to output shaft
woprev2 = woprev1; % speed using gear ratio
woprev1 = wo;
nTvec(n-1) = n*T; % store nT,wo into vectors for plotting
wovec(n-1) = wo;
end
nTvec = [0*T 1*T nTvec]; % put IC's into nT,w vectors
wovec = [0 0 wovec];
plot(nTvec, wovec, 'o')
grid;
xlabel('time (sec)');
ylabel('angular velocity (krpm)');
ttle = ['Motor Step Response for Kp=', num2str(Kp), ', Kd=', num2str(Kd), ...
', Ki=', num2str(Ki)];
title(ttle);
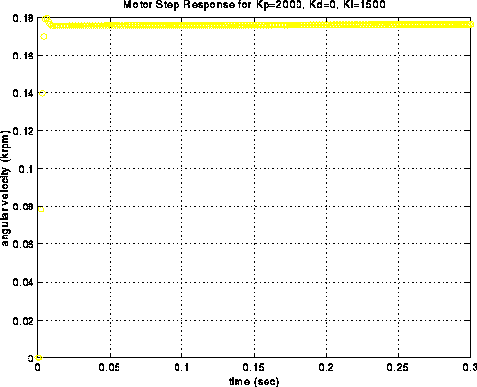
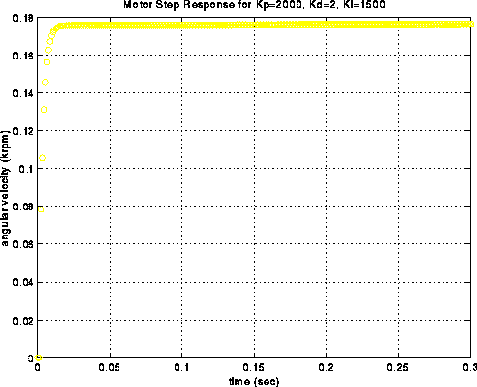
MATLAB Plots Generated from Three Separate Runs:


