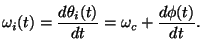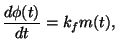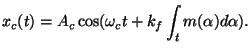Next: FM Demodulation
Up: Introduction
Previous: Introduction
In angle modulation, the amplitude of the signal is held constant and the phase is being varied with the message. An angle modulated signal is of the form:
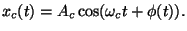 |
(1) |
The instantaneous phase of  is given by
is given by
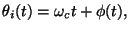 |
(2) |
and the instantaneous frequency is given by
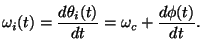 |
(3) |
Using this approach, if the message is proportional to  , which is the phase deviation, then we have phase modulation. If the message is proportional to
, which is the phase deviation, then we have phase modulation. If the message is proportional to
 , which is the frequency deviation, then we have frequency modulation.
In order to have phase modulation,
, which is the frequency deviation, then we have frequency modulation.
In order to have phase modulation,
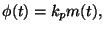 |
(4) |
where  is known as the deviation constant. For frequency modulation,
is known as the deviation constant. For frequency modulation,
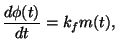 |
(5) |
where  is known as the frequency deviation constant. Consequently, an FM modulated signal is of the form
is known as the frequency deviation constant. Consequently, an FM modulated signal is of the form
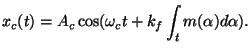 |
(6) |
An FM signal is shown in Figure 1
Figure 1:
Frequency modulation
 |



Next: FM Demodulation
Up: Introduction
Previous: Introduction
Copyright © 2003, Aly El-Osery
Last Modified 2003-11-02